You may think of symmetry as a term used
in art rather than mathematics. Symmetry is in fact used in
matematics both descriptiviely and as a tool for solving problems.
Three examples are given below to get a sense of what is meant by
symmetry and how it is used.
What is Symmetry?
Before we proceed we need to say what
symmetry is. Symmetry seems to be one of those things that you
can recognize but not define exactly. Consider the following
examples of symmetry.
How can there be a single definition to cover all these cases?
Definition (informal) of Symmetry:
Given a set of objects, an operation performed on the objects and a property of the set of objects, we say that we say that the property has symmetry with respect to the operation if after performing the operation the property remains unchanged.
For example, consider the letter A. Intuitively we would say that A is symmetric with respect to an axis going vertically through the center. To apply the definition we would take that axis and reflect the letter A on either side of the axis. Then the space occupied by the letter is symmetric with respect to reflection in the axis. Similarly, the space occupied by the letter C is symmetric with respect to reflection in a horizontal axis. What about the letter S? It does not have either vertical or horizontal symmetry. Can you think of an operation that will leave S occupying the same space? If you wrote S on a piece of paper and turned the paper upside down it would still be the letter S. We say that S is symmetric with respect to rotation by 180 degrees about the point in the center of the letter. How many different types of symmetry can you find for the letter X?
What about the table and lamp? Do you see a symmetry operation? Suppose we swapped the colors red and blue in the description. We would have an equivalent description. So we can say that the description is symmetric with respect to color swapping. At this point the symmetry of the equation should be apparent. Swapping the letters x and y in the equation satisfies the exact same condition.
We can now place AB of the original triangle on CB of the flipped triangle and the same for CB of the original triangle and AB of the flipped triangle. Since the vertices line up it follows that the two triangles are congruent and therefore angle A is congruent to angle C.
If pressed still further, we can express this argument in strictly Euclidean terms. Given three points A, B and C, the order of the vertices makes a difference, so triangle ABC is different from triangle CBA. From the given, we have that AB of the first triangle is congruent to CB of the second and that CB of the first triangle is congruent to AB of the second. The included angle B is congurent to itself so triangle ABC is congurent to triangle CBA by SAS, and therefore by corresponding parts of congruent triangles, angle A is congruent to angle C.
We are ready to examine three more involved examples of symmetry.
- The letters A, C, S and X
- A red table with a blue lamp next to a blue table with a red lamp
- The equation x2 + y2 = r2
How can there be a single definition to cover all these cases?
Definition (informal) of Symmetry:
Given a set of objects, an operation performed on the objects and a property of the set of objects, we say that we say that the property has symmetry with respect to the operation if after performing the operation the property remains unchanged.
For example, consider the letter A. Intuitively we would say that A is symmetric with respect to an axis going vertically through the center. To apply the definition we would take that axis and reflect the letter A on either side of the axis. Then the space occupied by the letter is symmetric with respect to reflection in the axis. Similarly, the space occupied by the letter C is symmetric with respect to reflection in a horizontal axis. What about the letter S? It does not have either vertical or horizontal symmetry. Can you think of an operation that will leave S occupying the same space? If you wrote S on a piece of paper and turned the paper upside down it would still be the letter S. We say that S is symmetric with respect to rotation by 180 degrees about the point in the center of the letter. How many different types of symmetry can you find for the letter X?
What about the table and lamp? Do you see a symmetry operation? Suppose we swapped the colors red and blue in the description. We would have an equivalent description. So we can say that the description is symmetric with respect to color swapping. At this point the symmetry of the equation should be apparent. Swapping the letters x and y in the equation satisfies the exact same condition.
An
Example from Euclicean Geometry
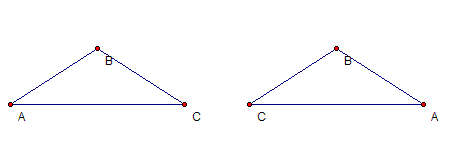
Suppose we are asked to
prove that the base angles of an isosceles triange are congruent.
We might start by saying that it really is intuitively
obvious. If pressed further, we might use a symmetry
argument. Suppose we flip the triangle around the vertex
angle, like so:

We can now place AB of the original triangle on CB of the flipped triangle and the same for CB of the original triangle and AB of the flipped triangle. Since the vertices line up it follows that the two triangles are congruent and therefore angle A is congruent to angle C.
If pressed still further, we can express this argument in strictly Euclidean terms. Given three points A, B and C, the order of the vertices makes a difference, so triangle ABC is different from triangle CBA. From the given, we have that AB of the first triangle is congruent to CB of the second and that CB of the first triangle is congruent to AB of the second. The included angle B is congurent to itself so triangle ABC is congurent to triangle CBA by SAS, and therefore by corresponding parts of congruent triangles, angle A is congruent to angle C.
Three Examples of the Use of Symmetry
We are ready to examine three more involved examples of symmetry.
Home