Review of Inverse Functions

Back

Home
Before
discussing
self-inverse let me
briefly review the idea of inverse function. We think of
addition
and subtraction as opposites as well as multiplication and division and
squaring and square roots. The definition of inverse function
is
a formalization of this idea. Consider the functions f(x) = x
+ 6
and g(x) = x - 6. If you add 6 to x and then
subtract 6 or
if you subtract and then add you end up where you
started,
with x. That is, g(f(x)) = f(g(x)) = x.
We say
that two functions f and g are inverses of each other if
f(g(x))
= g(f(x)) = x. Given a function f(x), if it has an inverse
the
inverse is designated as f-1(x).
Other pairs of inverse functions are f(x) = 6x and g(x) = x/6 and f(x)
= x2 and g(x) = sqrt(x).
Given an equation like y = 6x, the inverse can be found by solving for x in terms of y. This gives us x = y/6. This is just another way of saying that if we take 6x and divide by 6 we end where we started, with x.
Given a graph of a function f(x), it is easy to see the graph of f-1(x). Below is the graph of f(x) = x2 for x > 0.
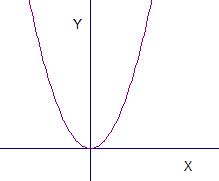
For any pair (x, y) on the graph such as (3, 9), the inverse function, square root of x, takes 9 to 3, and in general, if (a, b) is on the graph of f(x), (b, a) is on the graph of f-1(x). To see the points (b, a), it is only necessary to rotate the graph 90 degrees and flip it around so that the graph of square root of x is:
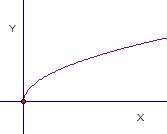
In order for this to be a function, I eliminated the values for the negative x values of the parabola.
Given an equation like y = 6x, the inverse can be found by solving for x in terms of y. This gives us x = y/6. This is just another way of saying that if we take 6x and divide by 6 we end where we started, with x.
Given a graph of a function f(x), it is easy to see the graph of f-1(x). Below is the graph of f(x) = x2 for x > 0.

For any pair (x, y) on the graph such as (3, 9), the inverse function, square root of x, takes 9 to 3, and in general, if (a, b) is on the graph of f(x), (b, a) is on the graph of f-1(x). To see the points (b, a), it is only necessary to rotate the graph 90 degrees and flip it around so that the graph of square root of x is:
In order for this to be a function, I eliminated the values for the negative x values of the parabola.
Self-Inverse
Functions
We know that for
any
constant a, the inverse of x/a is ax. What about
the function for the hyperbola fx(x) = a/x? In this case
f(f(x)) = x. a/x is its own inverse and so is a self-inverse function.
Using the definition of symmetry, the function f(x) = a/x is symmetric
with respect to the operation of inversion.
Below is a graph of the function 0.5/x:
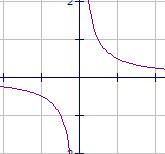
If we rotate the graph the way we rotated the graph above we end up with the same points.
Here is another way of visualizing the symmetry.
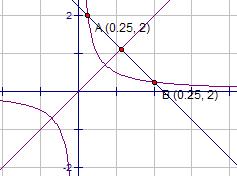
If we rotate the graph about the line y=x shown in the drawing we again get the same points. The graph is symmetric about the line y = x. This will be true of any self-inverse function. We know that for a point (a, b) for f(x) the point (b, a) is on the inverse f-1(x). Since f(x) = f-1(x) for self invese functions, for any point (a, b) on f(x) the point (b, a) must also be on f(x). In the picture, two such points A and B have been chosen. The midpoint of A and B is ((a + b)/2, (a + b)/2), which lies on the line y = x. The slope of the line through A and B is -1. The slope of the line y=x is 1. The product of the slopes is -1, meaning that the two lines are perpendicular, so that the line y = x is the perpendicular bisector of segment AB and consequently rotating about the line y=x swaps the positions of A and B.
If we look at the equation y = 0.5/x, it does not appear at first to hint at any symmetry. Can you think of a simple way of writing the equation so that the symmetry is revealed?
If we simply multiply both sides by x, we get xy = 0.5. The symmetry is now clear. Swapping x and y gives the same equation. Since x and y have the same role in the function, solving for x in terms of y will have the same form as the function expressing y in terms of x. It is now clear that the function y = 10 - x is a self-inverse since it is the same as x + y = 10. Using this property we can now easily generate self-inverse functions. For example, we can construct the self-inverse function xy = x + y. This says that for a given value of x, y is such that multiplying it by x is the same as adding it to x. If we solve for y we get y = x/(x-1).
Exercise: Verify that f(x) = x/(x - 1) is a self-inverse function.
Soltution: Substituting x/(x - 1) for x in x/(x - 1), f(f(x)) = x/(x - 1)/ (x/(x - 1) - 1) .
Simplifying the denominator, x/(x - 1) - 1 = (x - (x - 1)) /(x - 1) = 1/(x - 1), so we have x/(x - 1) / (11/ (x - 1)) = (x / (x - 1) )(x - 1) = x and so f(x) is self-inverse.
Exercise: Verify that f(x) = x/(x - 1) satisfies xf(x) = x + f(x)
Solution: xf(x) = x2/(x - 1).
x + f(x) = x + (x/(x - 1)) = (x(x - 1) + x)/ (x - 1) = (x2 - x + x)/(x - 1) = x2/(x - 1).
Below is a graph of the function 0.5/x:

If we rotate the graph the way we rotated the graph above we end up with the same points.
Here is another way of visualizing the symmetry.

If we rotate the graph about the line y=x shown in the drawing we again get the same points. The graph is symmetric about the line y = x. This will be true of any self-inverse function. We know that for a point (a, b) for f(x) the point (b, a) is on the inverse f-1(x). Since f(x) = f-1(x) for self invese functions, for any point (a, b) on f(x) the point (b, a) must also be on f(x). In the picture, two such points A and B have been chosen. The midpoint of A and B is ((a + b)/2, (a + b)/2), which lies on the line y = x. The slope of the line through A and B is -1. The slope of the line y=x is 1. The product of the slopes is -1, meaning that the two lines are perpendicular, so that the line y = x is the perpendicular bisector of segment AB and consequently rotating about the line y=x swaps the positions of A and B.
If we look at the equation y = 0.5/x, it does not appear at first to hint at any symmetry. Can you think of a simple way of writing the equation so that the symmetry is revealed?
If we simply multiply both sides by x, we get xy = 0.5. The symmetry is now clear. Swapping x and y gives the same equation. Since x and y have the same role in the function, solving for x in terms of y will have the same form as the function expressing y in terms of x. It is now clear that the function y = 10 - x is a self-inverse since it is the same as x + y = 10. Using this property we can now easily generate self-inverse functions. For example, we can construct the self-inverse function xy = x + y. This says that for a given value of x, y is such that multiplying it by x is the same as adding it to x. If we solve for y we get y = x/(x-1).
Exercise: Verify that f(x) = x/(x - 1) is a self-inverse function.
Soltution: Substituting x/(x - 1) for x in x/(x - 1), f(f(x)) = x/(x - 1)/ (x/(x - 1) - 1) .
Simplifying the denominator, x/(x - 1) - 1 = (x - (x - 1)) /(x - 1) = 1/(x - 1), so we have x/(x - 1) / (11/ (x - 1)) = (x / (x - 1) )(x - 1) = x and so f(x) is self-inverse.
Exercise: Verify that f(x) = x/(x - 1) satisfies xf(x) = x + f(x)
Solution: xf(x) = x2/(x - 1).
x + f(x) = x + (x/(x - 1)) = (x(x - 1) + x)/ (x - 1) = (x2 - x + x)/(x - 1) = x2/(x - 1).
Sines and
Cosines
Given the
equation cos(x) = sin(90 - x), how can we prove that
sin(x) = cos(90 - x)?
It is easy and requires no geometry or trig.
We observe that t(x) = 90 - x is self-inverse.
We then have cos(x) = sin(t(x)).
It then follows that cos(t(x)) = sin(t(t(x))= sin(x), since t is self-inverse.
That is cos(90 - x) = sin(x), which is what we wanted to prove.
sin(x) = cos(90 - x)?
It is easy and requires no geometry or trig.
We observe that t(x) = 90 - x is self-inverse.
We then have cos(x) = sin(t(x)).
It then follows that cos(t(x)) = sin(t(t(x))= sin(x), since t is self-inverse.
That is cos(90 - x) = sin(x), which is what we wanted to prove.
Another Way of
Looking at
Parabolas
Given the
function for the
parabola y = f(x) = -x2 + 10x +3, you
know that it has a maximum value which can be found by either
completing the square or, in calculus, taking the derivative.
If we assume that the extreme value of a parabola lies on the axis, we can
use the following method of determining the axis of symmetry to find the maximum value.
Write the function as y = x(10 - x) + 3. 10 - x is a self-invere function. Because of this,
f(10 - x) = (10 - x) x + 3 = f(x). For all x, f(10 - x) = f(x)
For any value x, we can find the other value, 10 - x, that has the same value for f. Another way of saying this is that for every point (x,y) on the parabola there is a point (10 - x, y). The midpoint of (x,y) and (10 - x,y) is ( (x+(10-x))/2, y) = (5,y). The line x=5 is a line of ymmetry for the parabola. The maximum value is for x = 5. f(5) = 28, so the maximum occurs at (5, 28).
The method also works if the coefficient of the x2 is 1 instead of -1. For example, consider f(x) = x2 + 10x + 3. We know the parabola in this case has a minimum value. f(x) can be rewritten as f(x) = -x(-10 - x) +3. f(-10 - x) = f(x). The axis of the parabola is the line x = -5.
Suppose that we had a function f(x) = g(a-x) + g(b+x). What can we do with this? Let's look at f(x-b). This moves the curve to the right by b and will get rid of the b value. We have f(x-b) = g(a-(x-b)) + g(b+(x-b)) = g((a+b)-x) + g(x). This is in the form we want. There willl be an axis of symmetry for f(x-b) at x = (a+b)/2. To get to our original function, we move to the left by b, which will move the axis of symmetry to the left as well. The axis of symmetry for f(x) is (a+b)/2 - b = (a-b)/2. Based on what we did before, going in the reverse direction suggests that f(a-b - x) = f(x). I leave it as an exercise to show from the definition of f(x), this is indeed the case.. If I had been more astute, I would have noticed it right away, without having to first look at f(x-b).
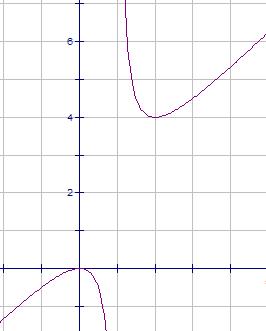
Now look at the equation y = x2/(x - 1). There is a discontinuity at x = 1, so the function divides into two pieces for x < 1 and x > 1. Let's look at the portion for x > 1. It should be clear that for x near 1 and for large values of x, the function goes to infinity, so we can suppose that it takes on a minimum value in between.
I came up with this function by taking the self-inverse function x/(x - 1) above and multiplying it by x. That is, f(x) = x(x/(x-1)). We can use this construction as in the case of the parabola to show that f(x/(x - 1)) = (x/(x - 1))x = f(x). If we assume that the function for x < 1 takes a minimum for only one value of x, then arguing as in the case for the parabola, at the minimum we must have x = x/(x - 1). Muliplying both sides by x - 1 we get x2 - x = x , x2 - 2x = 0, x(x - 2) = 0. For x > 1, the only solution is x = 2, for which f(x) = 4. Looking at the graph of the function it can be seen that we were correct in assuming that the function takes on a minimum at only one place and that the minimum does indeed occur for x = 2. The other solution for x(x - 2) =0, x = 0, is a maximum for the portion of the graph where x < 1.
Write the function as y = x(10 - x) + 3. 10 - x is a self-invere function. Because of this,
f(10 - x) = (10 - x) x + 3 = f(x). For all x, f(10 - x) = f(x)
For any value x, we can find the other value, 10 - x, that has the same value for f. Another way of saying this is that for every point (x,y) on the parabola there is a point (10 - x, y). The midpoint of (x,y) and (10 - x,y) is ( (x+(10-x))/2, y) = (5,y). The line x=5 is a line of ymmetry for the parabola. The maximum value is for x = 5. f(5) = 28, so the maximum occurs at (5, 28).
The method also works if the coefficient of the x2 is 1 instead of -1. For example, consider f(x) = x2 + 10x + 3. We know the parabola in this case has a minimum value. f(x) can be rewritten as f(x) = -x(-10 - x) +3. f(-10 - x) = f(x). The axis of the parabola is the line x = -5.
A Generalization
We
can generalize what we did with the parabola. Suppose we have f(x) =
arctan(x) + arctan(4 - x). Find the line of symmetry. This
may look scary, but it is easy to solve doing what we did for the
paraboloa. We have f(4 -x) = arctan(4-x) + arctan(4 - (4-x)) =
arctam(4-x) + arctan(x) = f(x). f(4-x) = f(x). Just as we
did above, we can say that there is an axis of symmetry for the line x
= 2. For any function g(x), f(x) = g(x) + g(a -x) has a line of
symmetry at x=a/2. This will hold for f(x)=g(x)g(a-x) or any
other function that can be written in terms of g(x) and g(a-x) which is
symmetric in g(x) and g(a-x).Suppose that we had a function f(x) = g(a-x) + g(b+x). What can we do with this? Let's look at f(x-b). This moves the curve to the right by b and will get rid of the b value. We have f(x-b) = g(a-(x-b)) + g(b+(x-b)) = g((a+b)-x) + g(x). This is in the form we want. There willl be an axis of symmetry for f(x-b) at x = (a+b)/2. To get to our original function, we move to the left by b, which will move the axis of symmetry to the left as well. The axis of symmetry for f(x) is (a+b)/2 - b = (a-b)/2. Based on what we did before, going in the reverse direction suggests that f(a-b - x) = f(x). I leave it as an exercise to show from the definition of f(x), this is indeed the case.. If I had been more astute, I would have noticed it right away, without having to first look at f(x-b).
Playing Around
with
Self-Inverse Functions
Now look at the equation y = x2/(x - 1). There is a discontinuity at x = 1, so the function divides into two pieces for x < 1 and x > 1. Let's look at the portion for x > 1. It should be clear that for x near 1 and for large values of x, the function goes to infinity, so we can suppose that it takes on a minimum value in between.
I came up with this function by taking the self-inverse function x/(x - 1) above and multiplying it by x. That is, f(x) = x(x/(x-1)). We can use this construction as in the case of the parabola to show that f(x/(x - 1)) = (x/(x - 1))x = f(x). If we assume that the function for x < 1 takes a minimum for only one value of x, then arguing as in the case for the parabola, at the minimum we must have x = x/(x - 1). Muliplying both sides by x - 1 we get x2 - x = x , x2 - 2x = 0, x(x - 2) = 0. For x > 1, the only solution is x = 2, for which f(x) = 4. Looking at the graph of the function it can be seen that we were correct in assuming that the function takes on a minimum at only one place and that the minimum does indeed occur for x = 2. The other solution for x(x - 2) =0, x = 0, is a maximum for the portion of the graph where x < 1.


Back
Home