In the days before
calculators and personal computers an engineer always had a slide rule
nearby. These days it is difficult to locate a slide rule outside of a
museum. I don't know how many of those who have used a slide rule ever
thought of it as an analog computer, but that is really what it is. As
such, I think that it is an ideal tool for teaching the mathematical
concept of transformations. With the proper scales, a slide rule can be
used not only to multiply but to find the third side of a right
triangle and add velocities relativistically. In order to introduce the
concepts that will be used, we will start with the simplest type of
slide rule - one that is made up of two ordinary rulers.
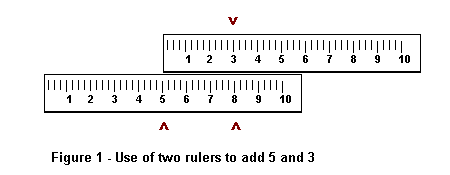
The addition slide rule was compared above to a mirror. Perhaps a more apt metaphor would be a translation.
Suppose you traveled back in time to the days of the Roman Empire. You notice someone doing arithmetic using Roman numerals and you want to verify your understanding of this numeric representation. Let T be the transformation from Arabic numerals to Roman numerals. According to what you were taught T(5) = V, T(III) = 3 and T(8) = VIII.
You observe that this particular person seems to be using ".." to stand for "+". You hand over a sheet of paper with V .. III written on it. When the person writes VIII on the paper this increases your confidence that the above transformation is correct. You have established a degree of internal consistency. We can think of addition as taking two input values to produce an output value. Since the output is determined by the inputs, for one process to be a translation of the other it is sufficient for equivalent inputs to result in equivalent outputs. (5+3) is the output of the Arabic numeral arithmetic. T(5)..T(3) is the output of the Roman numeral arithmetic. For the outputs to be equivalent we must have T(5)..T(3) = T(5+3) . If we could prove that in general T(X)..T(Y) = T(X+Y)then we could say that the one process is a translation of the other.
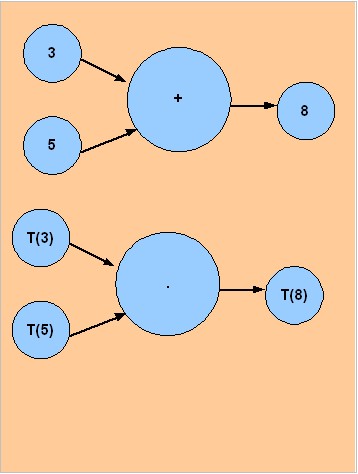
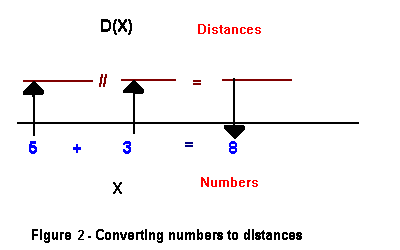
For the addition slide rule we have D(X) // D(Y) = D(X+Y) . The combining of distances is a translation of the addition of numbers. It does not matter that numbers and distances are different entities. Adding numbers is structually equivalent to combining distances. The next section states this in more formal terms.
The logarithmic function satisfies the relationship
log (x * y) = log(x) + log(y).
The log function is an isomorphism. It transforms a
multiplication problem into an addition problem. Since
addition of numbers is isomorphic to addition of
distances, consider the effect of applying the distance
function D to both sides of the equation.
D(log(x*y)) = D( log(x) + log(y) ) = D( log(x)) // D(log(y) )
D(log(x*y)) = D(log(x)) // D(log(y))
It follows that the transform (D log) formed by composing
the D and log transforms is an isomorphism. The same
process could be used to show that in general the
composition of two isomorphic transforms is an isomorphic transform -
the mirroring of the mirroring of a domain is itself a
mirroring of the domain;
the translation of a translation is a translation of the original.
The construction of a slide rule for multiplication
follows from the above equation. If the distance
that a number is placed is equal to the log of the
number then the result is the standard slide rule.
Figure 3 shows how the slide rule is used to
multiply 10 and 1000.
Shortly after their discovery it was realized that logarithm functions
loga(x)
were the inverse of exponential functions ax.
For convenience, let us write the exponential function as EXP(X) and
the logaritm function as LOG(X) for some common base a.
Since LOG(X) is an isomorphism and EXP(X) is its inverse, then by what
was shown above we get:
EXP(X+Y) = EXP(X) * EXP(Y),
which is an expression of the law of exponents.

Consider again the original formula for velocity
(c + w) / (c - w) = (c + u)/(c - u) * (c + v)/(c -v).
Let u & v be the sum of velocities u and v.
Let T(x) = (c + x)/(c - x).
Then T(u & v) = T(u)*T(v)
How do we add three velocities? In the example
of the person walking with velocity u in a
train traveling with velocity v, let s be the velocity
of the earth relative to the sun. What is the
velocity of the person relative to the sun?
Velocities can only be added two at a time. There
are two ways of doing this and we would hope that
they come out the same.
We could first find the velocity of the person
relative to the earth and then add this velocity to
the velocity of the earth relative to the sun.
This would give
T(s & (v & u)) = T(s) * T(v & u) = T(s) * (T(v) * T(u))
On the other hand we could first find the velocity of
the train relative to the sun and then add the
person's velocity. We then have
T((s & v) & u) = T(s & v) * T(u) = (T(s) * T(v)) * T(u).
The two values are of course the same. The reason
for this is that multiplication is associative, i. e.,
(a * b) * c = a * (b * c). We see that this causes
addition of velocities to be associative -
s & (u &v) = (s & u) &v.
The above argument could have been used for
any isomorphism. Thus we have the property
that isomorphisms preserve the associative
property just we showed earlier that they preserve
the commutative property. We could have used
this property to state immediately that it does
not matter which of the two ways the velocities
are added because multiplication is associative.
It could also have been argued that using the
velocity slide rule, it is obvious that it does not
make any difference in which order the velocities
are added. This is because the addition of distances
is both commutative and associative and any
calculation for which we can construct a slide
rule must therefore also be both commutative and
associative.
In the above formula for velocity addition it is
possible to solve for w to get
u & v = (u + v)/ (1 + u*v/c2).
To show that addition of velocities is associative
we could have then solved explicitly for both
(s & (v & u)) and ((s & v) & u), but this involves
a great deal more effort.
We can also apply the above results to the parallel resistor and
right triangle examples.
Using the notation in the section on right triangles, the
distance (x & y) that results from East and North displacements
of x and y is given by s(x & y) = s(x) + s(y). To generalize to
three dimensions we get s(s & y & z) = s(x) + s(y) + s(z).
For combining several parallel
resistors we get:
1/r = 1/r1 + 1/r2 + ... + 1/rn.
Although only a small portion of high school students is likely to
become computer programmers, most of them will probably be using
computers in one way or another. The distinction between program
developers and program users has been blurred by such software as
spreadsheets and database query programs. There are thus good practical
reasons for introducing Boolean algebra in high school. The DeMorgan
rules reveal a fundamental isomorphism that facilitates teaching this
subject and makes it more interesting.
The variables in Boolean algebra can take on only two values - TRUE or
FALSE and the principal operations are AND, OR and NOT. The variables
can stand for any statement; we are concerned with whether the
combination of such statements is either true or false.
The AND, OR and NOT operators agree with what common sense would say
they should be. NOT is the simplest operator. It takes only one
variable.
NOT X = FALSE if X is TRUE and TRUE if X is FALSE.
Because Boolean variables, unlike numerical values, take on only two
values we can completely specify the AND and OR operations with tables.
| Y | ||||
|---|---|---|---|---|
| TRUE | FALSE | |||
| X | ||||
| TRUE | TRUE | FALSE | ||
| FALSE | FALSE | FALSE | ||
Whenever possible, check to see if a result "makes sense". The
above table says that X AND Y is TRUE only if both X and Y are both TRUE,
in agreement with how the term AND is used in everyday use.
| Y | ||||
|---|---|---|---|---|
| TRUE | FALSE | |||
| X | ||||
| TRUE | TRUE | TRUE | ||
| FALSE | TRUE | FALSE | ||
The table for X OR Y says
that X OR Y is FALSE only if both X and Y are both FALSE.
One complication is that the word "or" in English can have two
different meanings; which one is being used can usually be determined
from the context of the statement. "or" can be defined as above or it
can be the same except that it is defined as FALSE when X and Y are
both TRUE. For example, if I say "Either candidate A or candidate B
will be the next president", it is understood that this rules out the
possibility of both A and B being the next president. This type of "or"
is referred to in logic as an exclusive or (XOR) and by way of contrast
OR is sometimes referred to as an inclusive or. In this section I will
only be dealing with the inclusive or.
Notice that the summary of the X OR Y table is the same as the summary
of the X AND Y table with the words TRUE and FALSE interchanged. This
suggests the following isomorphism, which is one of DeMorgan's two
rules:
NOT (X AND Y) = (NOT X) OR (NOT Y)
In plain language this says that if the statement X AND Y is not TRUE
then either X is FALSE or Y is FALSE. We can formally prove the
statement by using the two above tables to show that both sides of the
equation are equal for all four combinations of values for X and Y.
To get the other of DeMorgan's rules we apply the inverse of NOT to
show the isomorphism in the other direction. NOT is its own inverse so
we get:
NOT (X OR Y) = (NOT X) AND (NOT Y)
AND and OR are isomorphic. We could in principle discard OR from our
vocabulary and just use AND, though I would not recommend this unless
you are planning a career in politics. "It will rain today or tomorrow"
would become "It is not true that it will not rain today and it will
not rain tomorrow". There have been times, however, when I have used
DeMorgan's rules when programming to simplify statements.
The isomorphism simplifies proofs. We can use the table to show that
AND is commutative and associative. It follows immediately by
isomorphism that the same is true of OR.
We can go further. The fact
that NOT is the transform function for both AND and OR means that we
can apply both transforms simultaneously. For example, consider the
following distributive identity between AND and OR which is analogous
to the distributive operation of multiplication and addition:
X AND (Y OR Z) = (X AND Y) OR (X AND Z).
We can prove this statement by substituting all 8 combinations of X, Y
and Z. We should also test the reasonableness of the statement by using
an example.
"I will speak to Sarah and (I will speak to) John or Raymond." is the
same as "I will speak to Sarah and John or I will speak to Sarah and
Raymond."
Apply NOT to both sides of the equation. Using the AND isomorphism
gives the following on the left side.
NOT(X AND (Y OR Z)) = NOT X OR NOT (Y OR Z)
Applying the OR isomorphism gives
NOT X OR NOT (Y OR Z) = NOT X OR ((NOT Y) AND (NOT Z))
Each of the arguments has been negated and the ANDs and ORs have been
interchanged. The same happens on the right side of the equation. We get
NOT X OR ((NOT Y) AND (NOT Z)) =
((NOT X) OR (NOT Y)) AND ((NOT X) OR NOT Z)
We can get rid of the NOTs by setting X'=NOT X, Y'=NOT Y, Z'=NOT Z, so
that what end up is the same form as we started except the ANDs and ORs
have been interchanged:
X' OR (Y' AND Z') = (X' OR Y') AND (X' OR Z')
For every identity a new one can be created by interchanging AND and
OR.
The relationship between AND and OR is referred to as a duality. In
this case we have a duality between operators. There are different
types of duality but the general principle is that a dualism exists
when true statements can be generated from other true statements by
interchanging two terms.
Since, in general, xy
is not equal to yx,
there can not be slide rule scales for raising a number to a power if
we require both scales to be the same. However, if we remove the
requirement for isomorphism we can use two different scales to achieve
our purpose. We can create the slide rule scales if we can find two
different functions T and U that satisfy:
T(xy)
= T(x) + U(y)
We then create the slide rule having T(x) as the bottom scale and U(y)
as the top scale. Standard slide rules do this by having T(x) =
log(log(x)) and U(y) = log(y).
To see why this works, find log(log(xy)):
log(log(xy)) = log(y*log(x)) = log(y) + log(log(x)).