I discovered this way of finding the formula for a truncated pyramid or cone, known as a frustum, by using geometric series.  It is certainly not the standard way of deriving the equation, but I liked the way it works out.  I hope you will also.



  The two dimensional version of this is to find the area of a trapezoid, so let's start with finding the area of a trapezoid using geometric series and then extend the result to 3 dimensions.  The procedure used to find the area of a trapezoid will be a bit roundabout, but it will be very easy to extend the results to 3 dimensions.

Area of Trapezoid

The strategy for finding the area of the trapezoid is to build a triangle by layering copies of the trapezoid as show in the illustration.  We will use the geometric series to express the area T of the triangle in terms of the base trapezoid .  We will then find another geometric series to find the area of the triangle.  Equating  the two expressions for the area of the triangle allows us to solve for the area of the trapezoid.


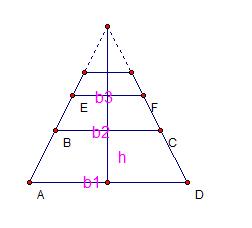
The trapezoid whose area A we want to find is ABCD given the lengths of the two bases b₁ and b₂ height h.  The trapezoid BEFC above ABCD has b₂ for its bottom base instead of b₁.  We want trapezoid BEFC to be similar to ABCD.  Since b₂ is the bottom base for BEFC, the scaling factor r = b₂/b₁. By taking the height of BEFC to be rh, it will be similar to ABCD.  The scaling factor for the next trapezoid applies the scaling factor r to BEFC and so has a scaling factor of r². b₃ = r² b₁ and for the nth trapezoid the scaling factor will be rⁿ.

The next thing we want to do is to find the area of the nth trapezoid in terms of A, r and n.  Since the scaling factor is rⁿ and area is proportional to the square of the scaling factor, the area of the nth trapeazoid is (rⁿ)²A =  (r²)ⁿA .  The area of the triangle is therefore:
T = A(1 + r² + (r²)² + (r²)³ + ...).  This is just an infinite geometric series in r², so we get area of of triangle =
T = A/(1 - r²)  --- ( equation 1)

Next, let's find the area of the triangle in terms of b₁ and h, using a geometric series to find the altitude H of the triangle in terms of h.  The scaling factor of r again applies, and so we get H = h(1 + r + r² + r³ + ...) = h/(1 - r).  

The area of the triangle is therefore T = 1/2 b₁ H = 1/2 b₁ h /(1 - r). ----- (equation 2)

We could at this point substitute  b₂/b₁ for r in the last expression for the area of the triangle, but let's keep it in terms of r and equate the two expressions for the area of the triangle.  Equating equation 1 with equation 2 gives

A/(1 - r²) =  1/2 b₁ h /(1 - r)
A = 1/2 b₁ h (1 - r²)/ (1 - r)

(1 - r²)/ (1 - r) simplifies to (1 + r).  Notice that (1 - r²)/ (1 - r)  is a speical case of the formula for geometric series.  (1 - r⁽ⁿ⁺¹⁾)/ (1 - r). In this case, n = 1 giving the very short geometric series 1 + r.  This idea will be more useful when we get to the three dimensional case.

Using the simplification, we get
A = 1/2 b₁ h (1 + r)
Substituting b₂/b₁ for r,  A = 1/2 b₁ h (1 + b₂/b₁) = 1/2 h (b₁ + b₂), which is the standard formula for the area of a trapezoid.

Volume of Frustum

It is now relatively easy to find the volume of a square truncated pyramid using the technique we used for trapezoids.



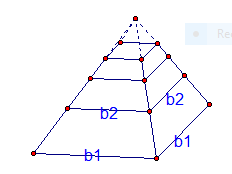
 We have b₁ for the lower base sides and b₂ for the upper base sides.  h is again the height and V is the volume that we want to find.  When we stack up the truncated bases in an infinte series we get a pyramid. The scaling factor is again  r = b₂/b₁ and once again the scaling factor for the nth figure is rⁿ.  The volume of the nth figure is proportional to the cube of the scaling factor, and so will be V(rⁿ)³ = V(r³)ⁿ.  The volume P of the pyramid is V(1 + r³ + (r³)² + (r³)³ + (r³)⁴ + ...), which is a geometric series in r³, so P = V/ (1 - r³).

The height of the pyramid is h/(1 - r) ,  Using this in the formula for the volume of a pyramid, P = 1/3 b₁² h./(1 - r)

Equating the two equations for P:
V/ (1 - r³) = 1/3 b₁² h./(1 - r)
V = 1/3 b₁² h (1 - r³)./(1 - r)
Recognizing (1 - r³)./(1 - r) as the formula for a geometric series, substituting for r and simplifying gives us:
V = 1/3 b₁² h (1 + r + r²) =  1/3 b₁² h (1 + b₂/b₁  +b₂²/b₁²)  =  1/3 h (b₁²+ b₁b₂ + b₂²).

Do you see a pattern in going from two dimensions to three dimensions?  What would you expect the formula to be in four dimensions?

Volume of Square Pyramid

We have been using the equation for the volume of a square pyramid as 1/3 b₁² H.  We can non-rigorously derive this formula based on the work we did with the frustum.   The assumption we will be will be making is that the volume is proportional to the height and to the area of the base.  You can convince yourself that this is the case if you consider the intersection of the altitude with many parallel planes perpendicular to the altitude and a fixed distance apart, We can approximate the volume as the sum of  rectangular prisms, each formed by one of the two bounding planes and the height between them.  If we stretch the height, we will get a propotional increase in the height between the planes.  Similarly, stretching each coordinate of the base will proportionately increase the volume .  Summarizing, assume that the volume is kb₁² H.  We want to show that k = 1/3.

Replacing 1/3 with k, we have the volume of the frustum as V  = k h b₁² (1 + r + r²) , where r = b₂/b₁  Consider what happens as b₂ approaches b₁ and r aproaches 1. We can't have r =1, because (1 - r³)/(1 - r)  = (1 + r + r²)  only holds when r does not equal 1.

As r approaches 1, the frustum becomes a rectangular prism with volume V = h b₁².  The frustum formula for r approaching 1 gives V  = k h b₁² (1 + r + r²) =  3 k h b₁².  Equating the rectangular prism equation with the frustum equaation gives  h b₁² =   3 k h b₁²   Simplifying, 3k = 1, k = 1/3, as we intended to show.