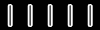Rotations and Revolutions

I would like to discuss an almost embarrassingly elementary principle that I think is nevertheless instructive for several reasons. Although the principle, which I will call the Principle of Relative Rotation, is elementary, I don't think that either it or its applications are quite so obvious. I didn't figure it out until after I left high school and I suspect that there are many others who are unaware of it. The Principle of Relative Rotation should be of general interest since it allows us to easily do things like determine how long it takes the Earth to complete a rotation (not quite 24 hours) and how long it takes the Moon to revolve around the Earth. I have looked in a few elementary books on kinematics and astronomy and although I found places where the principle could have been applied I could not find a discussion of the idea itself.

I will present this section as a history of my involvement with this principle. I do not do so in order to show off. On the contrary, I think anybody could do what I did. I want to show that mathematics is all around us and that we are all capable of exploring it.

The Problem

I became aware of the principle based on a problem I saw in a magazine advertisement: Take two coins of the same denomination and roll one along the edge of the other until it returns to the original position. How many times does the coin rotate? You might want to pause for a moment and try this on your own.

At the time it seemed obvious that the coin must make a single rotation. I was wrong. The coin makes two rotations. Why should this be?

First Attempt at a Solution

My first attempt at an explanation was to break the motion of the coin into two parts - one due to the path's length and one due to the path's shape.

If the coin rotates along a straight line for a distance equal to the circumference of the coin then it makes one rotation.

On the other hand, if the coin slides along the other coin but keeps the same point of contact then it also makes one rotation. The solution to the problem is to combine these two motions to get two rotations.

A Better Idea

I don't know about you, but I found this explanation to be unsatisfactory. It wasn't that it was wrong; it just didn't seem to be what I was looking for.

I wanted to relate this problem to the simple case where the coins act as two freely rotating enmeshed gears, with one turning once clockwise and the other turning once counterclockwise

It took me a while to realize that the answer was right in front of me and that it was as plain as 1 - (-1) = 2, which is not quite as obvious as 1 + 1 = 2.

If clockwise rotations are assigned positive numbers then counterclockwise numbers should be assigned negative numbers. The difference between a clockwise rotation and a counterclockwise rotation is 1 - (-1) = 2, which is the difference in the number of rotations in the problem, since one coin rotated twice and the other didn't rotate at all.

The simple case is not just related to the original problem. The two cases are equivalent, differing only in the vantage point of the observer.

If we take coins turning in opposite directions and place a tiny observer on the coin rotating counterclockwise, then what does this observer see? The observer will not be aware of the movement of its own coin just as we do not sense the movement of the Earth. When the two coins each rotate once, the other coin will appear to rotate twice clockwise. Further, the other coin will also appear to make a single clockwise revolution for the same reason that the rotation of the Earth makes it appear as if the sun revolves around the Earth.

The Principle of Relative Rotation

I could now formulate the Principle of Relative Rotation: The difference in the number of rotations of two objects is unchanged when the observer's reference frame is rotating.

This still left the problem of revolutions. How could we get from no revolutions to one revolution? Well, no revolutions is the same as zero revolutions, which falls between -1 and +1 rotation in the one case just as one revolution falls between 0 and 2 rotations in the other. Therefore, if revolutions are regarded as a special type of rotation, then they can be fit into the general principle.

Geometric Justification

To provide a geometric explanation we must first determine how to measure the amount of rotation.

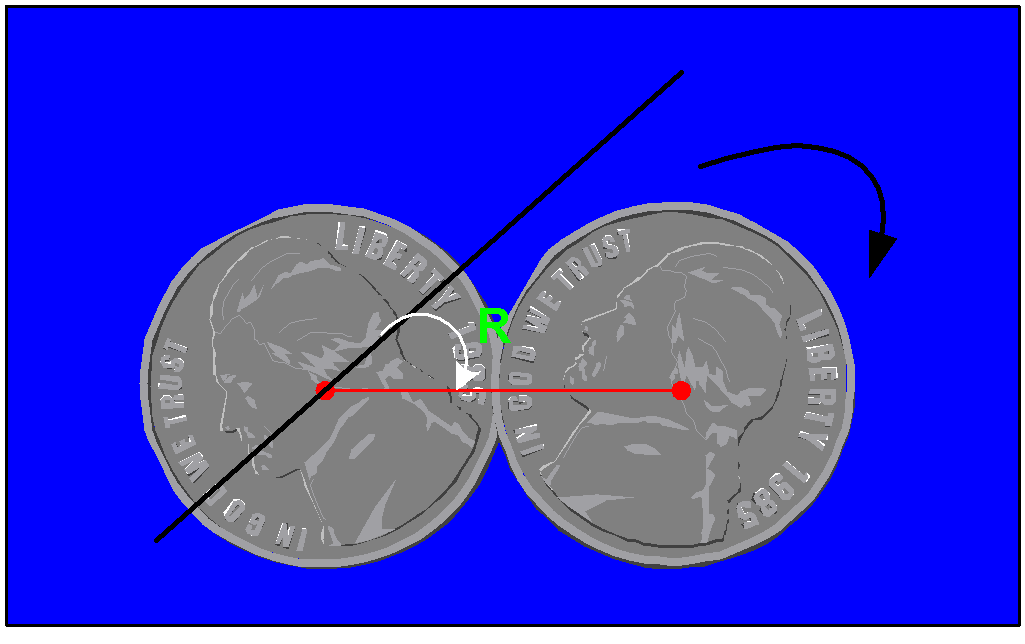
First we choose a base line in the reference system. Then we choose an angle reference line in the rotating object and measure its angle A with respect to the base line, as shown in the picture below on the left.

The amount of rotation is the difference in the angle A₁ that the angle reference line makes with the base line before rotating and the angle A₂ that it makes with the base line after rotating.

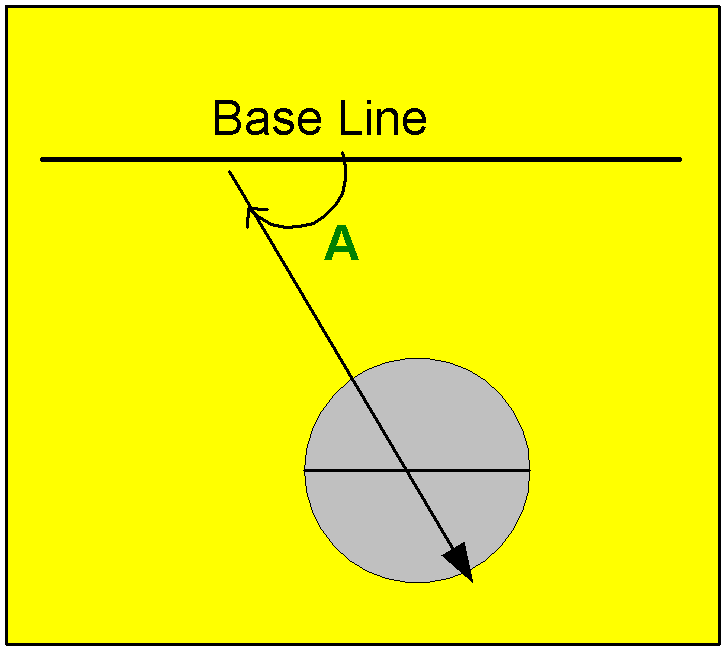
In the picture on the right there are two base lines B₁ and B₂, where B₂ has been rotated through an angle of R with respect to B₁. B₂ also goes through the intersection of B₁ and the angle reference line. In this case it is obvious that the angle A' that the angle reference line makes with respect to B₂is given by A' = A - R.

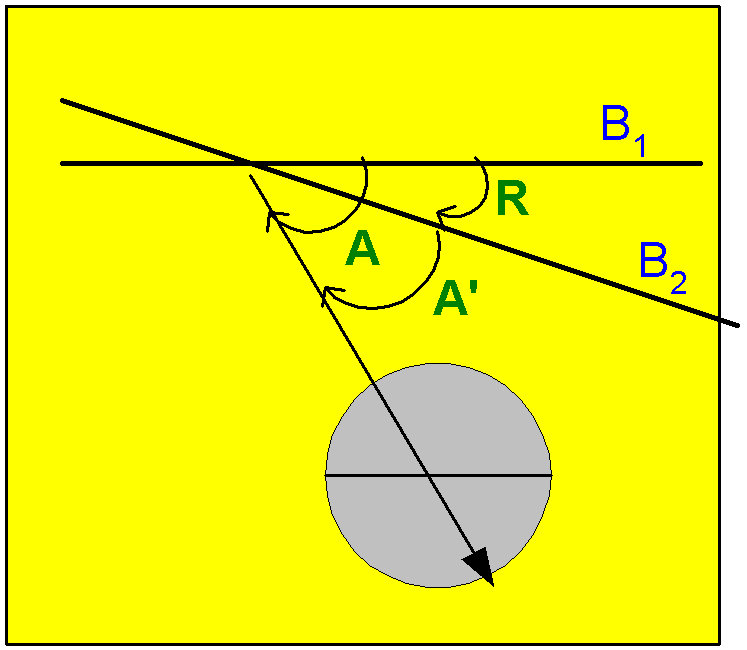
What if the second base line does not go through the intersection of the angle reference line with the first base line? The picture below illustrates this case.

Keeping the line B₂ parallel to its original orientation and sliding it to the right so that it goes through the intersection of B₁ with the angle reference line, the angles A' and R are unchanged and we get the previous case. Again A' = A - R.

Imagine that at the start of the rotational movement of several objects that the two base lines coincide. The initial angles therefore will be the same in both reference systems. If the second base line rotates through an angle R while the various other objects rotate, then in the second reference frame all the final angles will be reduced by R. The differences between initial and final angles will also be reduced by R. Thus all rotations in the second reference frame will be reduced by R. Therefore the difference between any two rotations will be the same in the second reference frame as in the first.

Yes, But What About Revolutions?

First we must determine what we mean by a revolution: Draw the line L connecting the centers of two objects O₁ and O₂. A revolution between O₁ and O₂ can be defined as the change in the angle that L makes with the base line.

Consider again the two coins rotating in opposite directions.

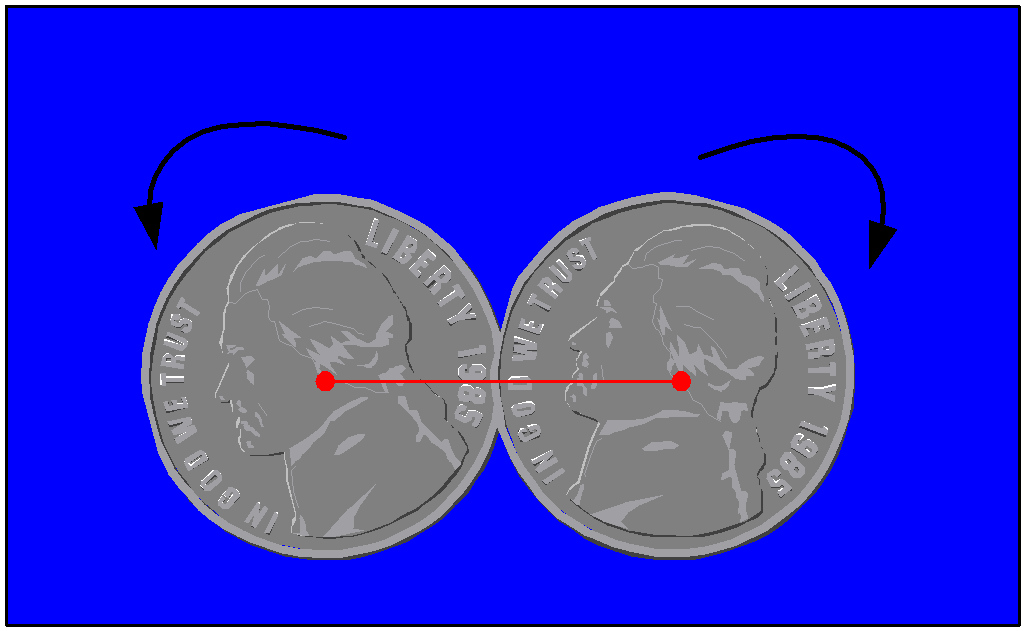
In the picture on the left the line joining the coin centers is shown. Both the base line and the line joining the centers remain fixed and so there are no revolutions.

In the picture on the right, the situation is shown as it appears to the observer on the counterclockwise moving coin. The line joining the centers appears to move clockwise and so the observer sees the other coin making a revolution.

We may think of a revolution as the rotation of the line joining the centers and therefore the Principle of Relative Rotation applies equally to it.

What Revolves Around What?

One thing that may strike you as odd about the definition of revolutions is that it does not provide any way of determining which object is revolving around which. There is, in fact, no need to make a distinction.

Consider a line in a plane. Rotate the line clockwise keeping one end fixed. Now go back to the original position and perform the rotation keeping the other end fixed. The change in the angle that the line makes with respect to a base line is the same in each case. Consider a revolution between two objects O₁ and O₂. If an observer on O₁ perceives O₂as revolving around O₁ by an angle R in a certain direction then the observer on O₂ will perceive O₁ as moving by R around O₂ in the same direction.

On to Bigger Things

Having mastered the rotation of coins I decided to take on the world, and the moon as well. It helped considerably that the planets and moons in the Solar System move in roughly the same plane.

When discussing the coins, I made the assumption that they were being viewed from above. If, for example, our observer were placed on the bottom of a coin then all rotations would be perceived as being in the opposite direction - clockwise would become counterclockwise and vice verse. In discussing Earth, the Northern and Southern Hemispheres are analogous to the top and bottom of a coin. In what follows the assumption will be made that earth-bound observers are in the Northern Hemisphere and observers in space are viewing from above the North Pole. Please excuse my hemispherist bias.

Earth Rotations

Consider first Earth rotations. Rotation of the Earth is not the same as a day. To see why, consider the diagram below, which represents the Earth revolving around the sun, as viewed from above the North Pole.

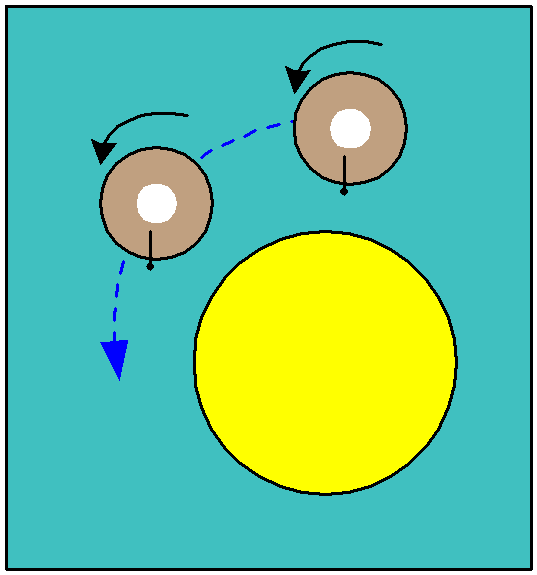
In the top position, the line on the circle representing Earth indicates a location where it is noon.

In the next position, the Earth has gone through a complete rotation but it is not yet noon at the specified location. The Earth will have to rotate a little further for this to happen. Thus a day is longer than a rotation.

The difference between a day and a rotation is one way of explaining the changes in the night sky during the course of a year. During a single rotation all of the constellations appear overhead. The only ones that are visible are the ones that are overhead at night and because rotations and days are out of synch, which stars appear at night will differ during the course of a year.

The number of Earth rotations in a year is calculated as follows. To an observer on Earth, the Earth makes no rotations and the sun appears to make 365 1 /4 clockwise revolutions around the Earth. We thus have:

revolutions - rotations = 365 1/4 - 0 = 365 1/4.

When viewed from outer space, the Earth is seen to go counterclockwise around the sun. Therefore, by the Principle of Relative Rotations:

revolutions - rotations = -1 - rotations = 365 1/4.

Earth rotations in a year = -366 1/4. The earth rotates 366 1/4 times counterclockwise in a year. The time to make a rotation can be found by dividing 366 1/4 into (365 1/4 days * 24 hours/day) yielding a rotation time of about 23 hours and 56 minutes.

Moon Revolutions

On Earth we observe that a lunar phase cycle, the time from one full moon to the next, takes 29.5 days. Both the sun and moon appear to move clockwise with the moon lagging behind. A phase cycle is the time required for the sun to appear to make a lap relative to the moon, so the quantity we are computing is sun revolutions - moon revolutions. The number of these in a year is (365 1/4)/ 29.5 = 12.38. We thus have:

sun-Earth revolutions - moon-Earth revolutions = 12.38.

From outer space, there is one counter clockwise sun-Earth revolution, so by the Principle of Relative Rotation,

-1 - moon-Earth revolutions = 12.38.

The moon makes 13.38 counterclockwise revolutions per year. The time to make one revolution is (365 1/4 days) / 13.38, or about 27.3 days.

Note that although the rotation of the Earth affects the apparent revolutions of both the sun and moon, the Earth's rotation was not involved in the above calculation, since both sun and moon are affected equally by it.

HOME