If you are not
already familiar with peg solitaire,here here is a link to a
description of the game.
Suppose that we want to play so that we end up with one peg remaining. We can use modular arithmetic to determine the possible positions for the final peg.
In order to explain how this works, I am going to start by attempting to use ordinary arithmetic to accomplish our aim. This attempt will not be successful, but the reason for the failure leads directly to why modular arithmetic, specifically mod 2 arithmetic, works.
Suppose we choose four holes on the board containing pegs that form a two by two square and we assign numbers to each of them. We might have something like:
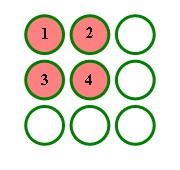
The sum of the values in the occupied holes is 1+2+3+4 = 10 . We want to assign numbers to the adjacent positions so that each hole will have a value that is equal to the sum of the two preceding positions, like so:
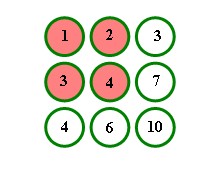
Now suppose we jump the peg in 1 to the peg in 3, leaving:
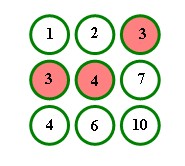
The two pegs in 1 and 2 have been replaced by a peg in 3, leaving the sum of the holes with pegs the same, 3+4+3 = 10. We can continue to do jumps, replacing the pegs in 3 and 4 by a peg in 7 and finally replacing pegs in 3 and 7 by 10, so that the value of the final peg is our initial sum of 10.
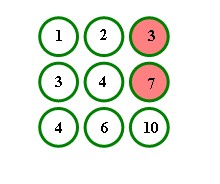
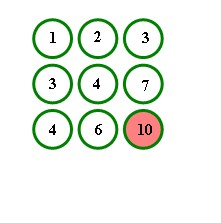
In general, however, the sum will not be preserved. Do you see why? It only works if we jump from left to right or top to bottom. If we move in the opposite directions the value of the two pegs is replaced by the subtraction of the two pegs involved in the jump.
For example, if we start as follows:
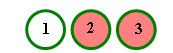 and jump to the left we end up
replacing 3 and 2 with 3 - 2 = 1.
and jump to the left we end up
replacing 3 and 2 with 3 - 2 = 1.
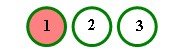
If we could make subtraction the same as addition, we would be able to preserve the sum of the filled holes. How can subtraction be the same as addition? It will if we do our arithmetic mod 2. In mod 2, we have only two numbers, 0 and 1. You can think of 1 as representing all odd numbers and 0 as representing all even numbers. Adding or subtracting an odd number has the same affect on the evenness or the oddness of the result. The same holds for even numbers. Stated more formally:
x+1 = x - 1 (mod 2)
x+ 0 = x - 0 (mod 2)
Suppose we start with two circles labeled with a one, as shown below. The circle to the right would be labeled 1 + 1 = 0 (mod 2). Going from the two circles on the right and moving to the left we get 0 +1 = 1 (mod 2)

If we start with 4 circles as before, numbering them with 0 and 1, we can number all the other holes with 0 and 1 so the sum will always be preserved. The only possible positions where there can be one remaining peg are the ones whose values matches this sum. You may think that this does not limit the possibilities very much, but we will show that by making use of symmetry we can zero in on the only two possible final positions.
In the picture below, I started by labeling the four red circles and the rest of the holes are numbered following the rule of having holes labeled with the sum of the two adjacent holes.
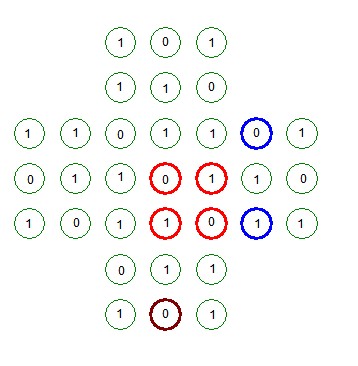
To find the sum, count the number of 1's in all holes except the center. There are 22, which is even, so the sum is 0. The only positions where the final peg can be are the ones labeled with 0. Note that these include the center hole. We can use symmetry to eliminate other positions. The two blue holes are equivalent. If we could get a peg to end up in one of them, we could alter the play so as to end up with a peg in the other. Since one of these holes has a 1, that eliminates both of them as possible positions for the last peg. When we are done, there will be one other type of position than can contain the last peg, indicated by the brown circle. Note that in order for a peg to end up in the center the final jump must be of two pegs in positions equivalent to the two holes between the brown circle and the center. If we jump in the opposite direction, we end up in the brown circle.
We could carry out a similar but more analysis for possible ways of ending up with 2 pegs. We know that the sum of these two positions would have to equal 0, so we are restricted to combinations of two holes that are either both labeled 0 or both labeled 1.
Suppose that we want to play so that we end up with one peg remaining. We can use modular arithmetic to determine the possible positions for the final peg.
In order to explain how this works, I am going to start by attempting to use ordinary arithmetic to accomplish our aim. This attempt will not be successful, but the reason for the failure leads directly to why modular arithmetic, specifically mod 2 arithmetic, works.
Suppose we choose four holes on the board containing pegs that form a two by two square and we assign numbers to each of them. We might have something like:

The sum of the values in the occupied holes is 1+2+3+4 = 10 . We want to assign numbers to the adjacent positions so that each hole will have a value that is equal to the sum of the two preceding positions, like so:

Now suppose we jump the peg in 1 to the peg in 3, leaving:

The two pegs in 1 and 2 have been replaced by a peg in 3, leaving the sum of the holes with pegs the same, 3+4+3 = 10. We can continue to do jumps, replacing the pegs in 3 and 4 by a peg in 7 and finally replacing pegs in 3 and 7 by 10, so that the value of the final peg is our initial sum of 10.


In general, however, the sum will not be preserved. Do you see why? It only works if we jump from left to right or top to bottom. If we move in the opposite directions the value of the two pegs is replaced by the subtraction of the two pegs involved in the jump.
For example, if we start as follows:
 and jump to the left we end up
replacing 3 and 2 with 3 - 2 = 1.
and jump to the left we end up
replacing 3 and 2 with 3 - 2 = 1.
If we could make subtraction the same as addition, we would be able to preserve the sum of the filled holes. How can subtraction be the same as addition? It will if we do our arithmetic mod 2. In mod 2, we have only two numbers, 0 and 1. You can think of 1 as representing all odd numbers and 0 as representing all even numbers. Adding or subtracting an odd number has the same affect on the evenness or the oddness of the result. The same holds for even numbers. Stated more formally:
x+1 = x - 1 (mod 2)
x+ 0 = x - 0 (mod 2)
Suppose we start with two circles labeled with a one, as shown below. The circle to the right would be labeled 1 + 1 = 0 (mod 2). Going from the two circles on the right and moving to the left we get 0 +1 = 1 (mod 2)

If we start with 4 circles as before, numbering them with 0 and 1, we can number all the other holes with 0 and 1 so the sum will always be preserved. The only possible positions where there can be one remaining peg are the ones whose values matches this sum. You may think that this does not limit the possibilities very much, but we will show that by making use of symmetry we can zero in on the only two possible final positions.
In the picture below, I started by labeling the four red circles and the rest of the holes are numbered following the rule of having holes labeled with the sum of the two adjacent holes.

To find the sum, count the number of 1's in all holes except the center. There are 22, which is even, so the sum is 0. The only positions where the final peg can be are the ones labeled with 0. Note that these include the center hole. We can use symmetry to eliminate other positions. The two blue holes are equivalent. If we could get a peg to end up in one of them, we could alter the play so as to end up with a peg in the other. Since one of these holes has a 1, that eliminates both of them as possible positions for the last peg. When we are done, there will be one other type of position than can contain the last peg, indicated by the brown circle. Note that in order for a peg to end up in the center the final jump must be of two pegs in positions equivalent to the two holes between the brown circle and the center. If we jump in the opposite direction, we end up in the brown circle.
We could carry out a similar but more analysis for possible ways of ending up with 2 pegs. We know that the sum of these two positions would have to equal 0, so we are restricted to combinations of two holes that are either both labeled 0 or both labeled 1.